POLYNÔMES

POLYNÔMES

La théorie des équations et des polynômes a été le propos essentiel de l’algèbre jusqu’au XIX^e siècle (cf. ÉQUATIONS ALGÉBRIQUES, ALGÈBRE) et est à la base de la théorie des corps et de la théorie des nombres algébriques. Nous nous sommes limités ici à une construction formelle des objets mathématiques considérés, qui fait apparaître, sous le vocable «polynômes», l’existence de deux notions distinctes: les polynômes formels et les fonctions polynomiales. Cet article élémentaire pourra aussi servir d’introduction au maniement des notations abstraites.

Polynômes formels

La notion de polynôme est familière, mais on s’est contenté pendant fort longtemps de décrire des règles de calcul sans définir véritablement les objets mathématiques considérés. On trouve couramment des définitions comme: «Un monôme entier en la variable x est une expression de la forme Axⁿ , A étant un coefficient numérique et n un entier positif»; «Un polynôme en la variable x est une somme qui ne peut être composée (sic ) que de nombres et de monômes entiers». Puis suit l’énumération des règles de calcul sur ces objets.

La construction des polynômes donnée ici illustre, dans le cadre simple de l’algèbre élémentaire, la manière dont le mathématicien formalise, en suivant une voie qui peut sembler a priori déroutante, voire artificielle, certaines notions tenues pour «évidentes» ou «intuitives».

Définition

Soit A un anneau commutatif unitaire ^{[cf. ANNEAUX ET ALGÈBRES]}. On appelle polynôme à une indéterminée (cette terminologie sera justifiée plus loin) à coefficients dans A toute suite:

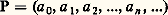d’élément de A nuls sauf au plus un nombre fini d’entre eux (c’est-à-dire tous nuls à partir d’un certain rang). Les éléments aⁱ sont les coefficients du polynôme P.

Les polynômes étant définis comme des cas particuliers de suites (c’est-à-dire d’applications de l’ensemble N des entiers naturels dans A), deux tels polynômes sont donc égaux si et seulement s’ils ont les mêmes coefficients.

Anneau des polynômes

Nous allons maintenant définir formellement l’addition et la multiplication. Soit:

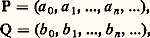deux polynômes à coefficients dans A. On appelle somme et produit de P et Q respectivement les polynômes:

et:

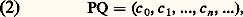avec: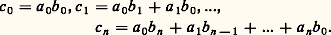

Il est facile de vérifier que l’ensemble des polynômes considérés est ainsi muni d’une structure d’anneau commutatif unitaire; nous désignerons provisoirement cet anneau par L. On va montrer qu’on peut «identifier» A à un sous-anneau de l’anneau L en remarquant pour cela que l’application:

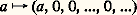est un isomorphisme d’anneau de A sur le sous-anneau A de L formé des polynômes dont tous les coefficients de rang 閭 2 sont nuls. Il est donc équivalent de «calculer» dans A ou de faire ces calculs sur les éléments correspondants de A , et nous identifierons ces deux anneaux en utilisant l’écriture abrégée:

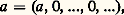pour tout a 捻 A. Pour cette raison, les éléments de A sont appelés des constantes , ou des polynômes constants .

Remarquons que, si a est un polynôme constant et P un polynôme quelconque, la multiplication de P par a revient à multiplier tous les coefficients de P par a . Dans le cas où A est un corps, cette «multiplication scalaire» (a , P) 料 a P munit l’anneau des polynômes à coefficients dans A d’une structure d’algèbre commutative sur le corps A.

Notion d’indéterminée

Désignons par X le polynôme:

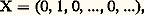dont tous les coefficients sont nuls, sauf le second coefficient, qui est égal à l’élément 1 de l’anneau A. Il résulte de la définition (2) de la multiplication que l’on a:

et, plus généralement, pour tout entier n 礪 0,

où 嗀^ij est le symbole de Kronecker (égal à 1 si i = j et à 0 si i j ). Si on a:

avec a^p = 0 pour p 礪 n et aⁿ 0, on obtient donc, en appliquant les définitions:

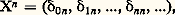
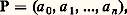
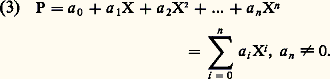Le nombre n qui figure dans la formule (3) s’appelle le degré du polynôme P, noté d⁰(P); tout polynôme différent du polynôme nul a un degré bien déterminé, et l’écriture (3), appelée développement de P suivant les puissances croissantes, est unique. L’anneau des polynômes étant commutatif, on pourrait tout aussi bien «ordonner P suivant les puissances décroissantes» en écrivant:

Pour éviter des cas d’exception, on pose souvent d⁰(0) = 漣 秊, symbole formel régi par les conventions suivantes: pour tout entier naturel n , on pose 漣 秊 麗 n et n + (face=F0019 漣 秊) = 漣 秊; (face=F0019 漣 秊) + (face=F0019 漣 秊) = 漣 秊. On peut alors énoncer, quels que soient les polynômes P et Q, des résultats tels que: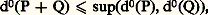

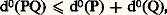avec égalité si d⁰(P) d⁰(Q), et:

avec égalité si A est un anneau d’intégrité.

La notation (3) justifie la terminologie de polynôme «à une indéterminée» et la notation A[X] que l’on utilise pour désigner l’anneau des polynômes à une indéterminée à coefficients dans A. Il est clair que la lettre X que l’on utilise pour désigner le polynôme (0, 1, 0, ...) est arbitraire, en ce sens que, si, dans un texte mathématique, les lettres X et Y sont «disponibles», c’est-à-dire si elles n’ont pas encore été employées précédemment, on a A[X] = A[Y].

La construction formelle est maintenant terminée et les polynômes sont complètement définis. Il nous suffit de retenir que ce sont des objets mathématiques qui s’écrivent de manière unique sous la forme (3) et qui obéissent aux règles usuelles de calcul dans un anneau.

Remarquons pour terminer que, si A est un corps,

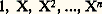est une base de l’espace vectoriel (sur A) des polynômes de dimension 諒 n , espace qui est donc de dimension n + 1.

Dérivation formelle

L’examen des règles classiques de dérivation des fonctions numériques conduit à une approche formelle de la dérivation dans un anneau. On appelle dérivation d’un anneau commutatif unitaire B une application:

telle que, quels que soient P et Q 捻 B, on ait: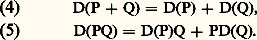

On s’intéressera ici à l’unique dérivation de B = A[X] telle que:

pour tout polynôme constant a 捻 A. Si P = a ⁰ + a ¹ X + ... + aⁿ Xⁿ , il résulte immédiatement des conditions (4) et (5) que l’on a: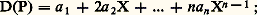

on note souvent D(P) = P . Par récurrence, on alors la définition:

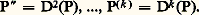Polynômes à plusieurs indéterminées

Si A est un anneau commutatif unitaire, il en est de même de l’anneau B = A[X] des polynômes à une indéterminée à coefficients dans A. On peut donc considérer l’anneau C des polynômes à une indéterminée à coefficients dans B, soit:

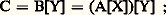il faut employer une autre lettre, Y, car X a déjà été utilisé. L’anneau B s’identifie à un sous-anneau de C et tout élément non nul de C s’écrit de manière unique:

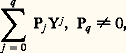où P^j 捻 A[X], soit:

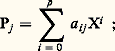d’après les règles de calcul dans l’anneau C, tout polynôme non nul de C s’écrit donc de manière unique sous la forme:

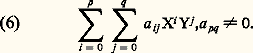La symétrie qui apparaît dans cette formule suggère la notation symétrique C = A[X,Y] pour désigner l’anneau des polynômes à deux indéterminées à coefficients dans A. On définit de la manière usuelle le degré total d’un tel polynôme, égal à p + q si le polynôme est sous la forme (6), les degrés partiels en X et en Y, égaux respectivement à p et q dans (6), et les dérivations partielles formelles.

La construction précédente s’étend sans difficulté par récurrence pour définir l’anneau A[X¹, ..., Xⁿ ] des polynômes à n variables à coefficients dans A.

Si A est un anneau d’intégrité, les anneaux de polynômes A[X¹, ..., Xⁿ ] sont des anneaux d’intégrité. Dans le cas particulier où A = K est un corps commutatif, le corps des fractions (cf. ANNEAUX COMMUTATIFS, chap. 1, et CORPS, chap. 2) de l’anneau K[X¹, ..., Xⁿ ] est le corps des fractions rationnelles à n variables à coefficients dans K; on le note traditionnellement K(X¹, ..., Xⁿ ).

Division euclidienne

Nous supposerons dans ce qui suit que A = K est un corps commutatif. L’anneau K[X] possède alors des propriétés arithmétiques très voisines de celles de l’anneau Z des entiers relatifs. Cela traduit le fait que l’un et l’autre sont des anneaux principaux et on peut dire que cette notion unificatrice d’anneau principal est née essentiellement de la répétition parfaite, pour l’anneau K[X], de toutes les considérations de divisibilité valables dans Z (cf. ANNEAUX COMMUTATIFS, chap. 2). Comme pour Z, la démonstration du fait que tout idéal est principal repose sur l’existence d’une division euclidienne : Si A et B 捻 K[X], il existe des polynômes Q et R déterminés de manière unique tels que:

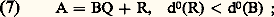le cas R = 0 exprime que A est un multiple de B. On voit ici l’intérêt de la convention d⁰(0) = 漣 秊, qui nous évite un cas d’exception.

Soit I un idéal de K[X]. Nous pouvons supposer I 0 et nous choisissons dans I un polynôme B 0 de degré minimum. Soit A 捻 I; la division euclidienne (7) de A par B entraîne que R = A 漣 BQ appartient à I puisque I est un idéal qui contient A et B. L’inégalité d⁰(R) 麗 d⁰(B) entraîne R = 0 puisque B est de degré minimum parmi les polynômes 0. Ainsi l’idéal I est formé des multiples du polynôme B et est donc principal.

La structure arithmétique des anneaux de polynômes à plusieurs indéterminées est plus compliquée et nous renvoyons à l’article ANNEAUX COMMUTATIFS pour des indications sur ce sujet.

Fonctions polynomiales

À l’exception de tout ce qui concerne les racines, les résultats qui seront énoncés dans le présent chapitre s’étendent facilement au cas des polynômes à plusieurs indéterminées; nous nous contenterons de les énoncer pour les polynômes à une indéterminée.

Fonction polynomiale associée à un polynôme formel

Soit A un anneau commutatif unitaire et: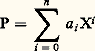

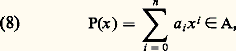un élément de A[X] écrit sous la forme (3). On appelle valeur de P sur un élément x 捻 A l’élément:

et fonction polynomiale associée à P l’application P: AA définie par P(x ) = P(x ); dans la pratique, on désigne encore par P cette fonction polynomiale.

Les fonctions polynomiales, c’est-à-dire les applications de A dans A pouvant s’obtenir à partir des éléments de A[X], forment un anneau commutatif unitaire, et l’application de K[X] dans cet anneau qui à tout polynôme formel associe la fonction polynomiale correspondante est un homomorphisme (par définition surjectif) d’anneaux. Si A est un anneau d’intégrité infini, cet homomorphisme est en fait un isomorphisme , c’est-à-dire que deux polynômes P et Q 捻 A[X] sont égaux si et seulement si P(x ) = Q(x ) pour tout x 捻 A. Pour obtenir un contre-exemple, il suffit de prendre pour A le corps fini0, 1, 2 des classes d’entiers modulo 3; le polynôme non nul:

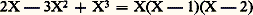prend la valeur 0 en tout point de A.

Remarque

Soit L un sur-anneau de l’anneau A. La formule (8) permet de définir P(x ) pour tout x 捻 L et de définir ainsi une application polynomiale, dite encore associée à P, de L dans L. Cette remarque va nous permettre de préciser un point de notation. Prenons pour L le sur-anneau A[X]; si Q 捻 A[X], la notation P(Q) désigne un élément de A[X] qui s’obtient en «substituant Q à X» et en développant les puissances de Q obtenues, en tenant compte des règles de calcul dans A[X]. Si on prend, en particulier, Q = X, on obtient le polynôme P lui-même, soit P(X) = P, ce qui nous permet d’utiliser indifféremment, pour désigner un polynôme, la notation P ou la notation P(X).

Prenant l’anneau A[X, Y] des polynômes à deux indéterminées pour sur-anneau, on peut donc définir P(X + Y) 捻 A[X, Y] pour tout P 捻 K[X]. La «formule de Taylor» s’écrit ici, si P est de degré n ,

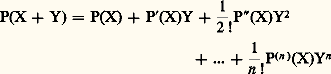où les dérivations qui figurent sont les dérivées formelles définies au chapitre 1.

Racines

Soit P 捻 A[X] et a un élément de A. La division euclidienne de P par X 漣 a s’écrit:

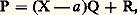avec d⁰(R) 麗 d⁰(X 漣 a ) = 1; donc R est un polynôme constant. Prenant les valeurs des deux membres en a , on a P(a ) = R, d’où l’égalité:

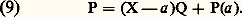On dit que l’élément a 捻 A est une racine du polynôme P si P(a ) = 0. D’après (9), cela équivaut à avoir P divisible par le polynôme du premier degré X 漣 a . On appelle ordre de mulplicité de la racine a le plus grand entier h tel que (X 漣 a )^h divise P; ainsi, dire que a est racine d’ordre k du polynôme P équivaut à affirmer: P = (X 漣 a )^k Q, l’élément a n’étant pas racine du polynôme Q.

Nous renvoyons aux articles CORPS et ÉQUATIONS ALGÉBRIQUES pour une étude détaillée des racines dans le cas où A est un corps commutatif. Terminons sur un résultat valable pour les anneaux d’intégrité: Si A est un anneau d’intégrité (unitaire) et si P 捻 A[X] est de degré 諒 n , P 0, la somme des ordres de multiplicité de P dans A est 諒 n . Il en résulte que, si P et Q 捻 A[X] sont tous deux de degré 諒 n et prennent des valeurs égales sur n + 1 éléments de A, alors P = Q.

Si K est un corps, on en déduit qu’il existe un polynôme de degré n et un seul prenant des valeurs données bⁱ 捻 K sur n éléments distincts donnés aⁱ 捻 K, i = 1, ..., n . On doit à Lagrange son expression sous la forme:

où Rⁱ (X) est le polynôme: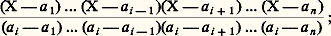

nous renvoyons à l’article représentation et approximation des FONCTIONS pour plus de précisions sur l’interpolation polynomiale. Remarquons que Rⁱ (X) est l’unique polynôme de degré n tel que:

où 嗀^ij est le symbole de Kronecker.

Encyclopédie Universelle. 2012.